Hãy tìm tổng lớn nhất của đường đi với tam giác lớn
Problem PE018-Maximum-path-sum-I
By starting at the top of the triangle below and moving to adjacent numbers on the row below, the maximum total from top to bottom is 23.
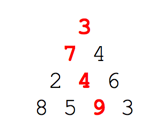
That is, 3 + 7 + 4 + 9 = 23.
Find the maximum total from top to bottom of the triangle below:

NOTE: As there are only 16384 routes, it is possible to solve this problem by trying every route. However, Problem 67, is the same challenge with a triangle containing one-hundred rows; it cannot be solved by brute force, and requires a clever method! ;o)
Đề bài
Đứng từ đỉnh của tam giác, bắt đầu di chuyển xuống dưới, giá trị nào cho tổng với giá trị trước đó lớn hơn sẽ được ưu tiên di chuyển vào.

Với ví dụ này: 3 + 7 + 4 + 9 = 23.
Hãy tìm tổng lớn nhất của đường đi với tam giác lớn dưới đây:

Phân tích đề bài:
Với tam giác nhỏ đầu tiên:
3
7 4
2 4 6
8 5 9 3
Ta thấy đáy của tam giác là 4 số, nếu đưa các giá trị của tam giác vào một ma trận 4 * 4 ta thu được một ma trận:
3 0 0 0
7 4 0 0
2 4 6 0
8 5 9 3
Nếu tính theo đường đi sẽ là
3 0 0 0
7 4 0 0
2 4 6 0
8 5 9 3
Nếu đặt 3 ở trên cùng là đỉnh (0,0), 3 ở dưới cùng là gốc (3,3).
Quá trình di chuyển và so sánh đường đi được mô tả:
(0,0) –> (1,0) vs (1,1): (1,0)
(1,0) –> (2,0) vs (2,1): (2,1)
(2,1) –> (3, 1) vs (3, 2): (3,2)
(3,2) –> END.
Ta thấy (x, y) luôn được so sánh với 2 giá trị liền dưới (x + 1, y) và (x + 1, y + 1)
Chương trình dừng lại khi x == lenght.
Với bài toán này, việc đầu tiên là chúng ta khởi tạo một list 2 chiều lưu trữ tam giác lớn.
[
[75, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[95, 64, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[17, 47, 82, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[18, 35, 87, 10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[20, 4, 82, 47, 65, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[19, 1, 23, 75, 3, 34, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[88, 2, 77, 73, 7, 63, 67, 0, 0, 0, 0, 0, 0, 0, 0],
[99, 65, 4, 28, 6, 16, 70, 92, 0, 0, 0, 0, 0, 0, 0],
[41, 41, 26, 56, 83, 40, 80, 70, 33, 0, 0, 0, 0, 0, 0],
[41, 48, 72, 33, 47, 32, 37, 16, 94, 29, 0, 0, 0, 0, 0],
[53, 71, 44, 65, 25, 43, 91, 52, 97, 51, 14, 0, 0, 0, 0],
[70, 11, 33, 28, 77, 73, 17, 78, 39, 68, 17, 57, 0, 0, 0],
[91, 71, 52, 38, 17, 14, 91, 43, 58, 50, 27, 29, 48, 0, 0],
[63, 66, 4, 68, 89, 53, 67, 30, 73, 16, 69, 87, 40, 31, 0],
[4, 62, 98, 27, 23, 9, 70, 98, 73, 93, 38, 53, 60, 4, 23]
]
GIRD = [
[75, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[95, 64, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[17, 47, 82, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[18, 35, 87, 10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[20, 4, 82, 47, 65, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[19, 1, 23, 75, 3, 34, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[88, 2, 77, 73, 7, 63, 67, 0, 0, 0, 0, 0, 0, 0, 0],
[99, 65, 4, 28, 6, 16, 70, 92, 0, 0, 0, 0, 0, 0, 0],
[41, 41, 26, 56, 83, 40, 80, 70, 33, 0, 0, 0, 0, 0, 0],
[41, 48, 72, 33, 47, 32, 37, 16, 94, 29, 0, 0, 0, 0, 0],
[53, 71, 44, 65, 25, 43, 91, 52, 97, 51, 14, 0, 0, 0, 0],
[70, 11, 33, 28, 77, 73, 17, 78, 39, 68, 17, 57, 0, 0, 0],
[91, 71, 52, 38, 17, 14, 91, 43, 58, 50, 27, 29, 48, 0, 0],
[63, 66, 4, 68, 89, 53, 67, 30, 73, 16, 69, 87, 40, 31, 0],
[4, 62, 98, 27, 23, 9, 70, 98, 73, 93, 38, 53, 60, 4, 23]]
def find_maximum_path():
max_lenght = len(GIRD[0])
x, y = 0, 0
path = [75]
for index in range(0, max_lenght - 1):
if x + 1 <= max_lenght and y + 1 <= max_lenght:
if GIRD[x+1][y] > GIRD[x+1][y+1]:
path.append(GIRD[x + 1][y])
x, y = x+1, y
else:
path.append(GIRD[x + 1][y + 1])
x, y = x + 1, y + 1
else:
path.append(GIRD[x + 1][y])
print(index, path)
return sum(path)
if __name__ == "__main__":
import time
start = time.time()
result = find_maximum_path()
done = time.time()
print("The maximum path sum: {}".format(result))
elapsed = done - start
print("elapsed time: {}s".format(elapsed))
Kết quả chạy trên máy của tôi:
0 [75, 95]
1 [75, 95, 47]
2 [75, 95, 47, 87]
3 [75, 95, 47, 87, 82]
4 [75, 95, 47, 87, 82, 75]
5 [75, 95, 47, 87, 82, 75, 73]
6 [75, 95, 47, 87, 82, 75, 73, 28]
7 [75, 95, 47, 87, 82, 75, 73, 28, 83]
8 [75, 95, 47, 87, 82, 75, 73, 28, 83, 47]
9 [75, 95, 47, 87, 82, 75, 73, 28, 83, 47, 43]
10 [75, 95, 47, 87, 82, 75, 73, 28, 83, 47, 43, 73]
11 [75, 95, 47, 87, 82, 75, 73, 28, 83, 47, 43, 73, 91]
12 [75, 95, 47, 87, 82, 75, 73, 28, 83, 47, 43, 73, 91, 67]
13 [75, 95, 47, 87, 82, 75, 73, 28, 83, 47, 43, 73, 91, 67, 98]
[75, 95, 47, 87, 82, 75, 73, 28, 83, 47, 43, 73, 91, 67, 98]
The maximum path sum: 1064
elapsed time: 0.00021004676818847656s
khi submit lên project euler, tôi thấy kết quả của mình sai.
Tất nhiên là không thể hiểu được điều gì đang diễn ra.
Tôi đã thử dùng phương pháp “rubber duck debugging” với dữ liệu ban đầu và thấy mình vẫn đúng.
Cuối cùng tôi chợt nhận ra….bài toán này không đơn giản chút nào. Có nhiều đáp án để bài toán hoàn thành và cái cách tôi đưa ra chưa phải là phương án đưa ra đáp án chính xác.
Và tôi nhận ra lỗi của tôi ở ngay dòng thứ 2
[75, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [95, 64, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [17, 47, 82, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [18, 35, 87, 10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
75 + 95 + 47 = 217 < 75 + 64 + 82 = 221
Đập bỏ phần so sánh 2 so sánh 2 số ở next-step đi, sau đó sử dụng phương án vét cạn cho toàn bộ đường đi. Cách làm này khá tệ để giải quyết.
Wait!
Đề bài chỉ yêu cầu lấy ra kết quả thay vì lấy ra danh sách các số. Vậy thay vì so sánh và cộng dần từ trên xuống thì ta so sánh và cộng dần từ dưới lên để tạo thành một tam giác mới.
a
b c
Với tam giác gồm 3 số kia, từ a đi xuống có thể 2 đường: a –> b hoặc a –> c
Nếu a chưa phải là đỉnh trên cùng, có thể thay thế a thành a + max(b,c)
Áp dụng vào tam giác nhỏ:
3
7 4
2 4 6
8 5 9 3
2 + max(8, 5) = 2 + 8 = 10
4 + max(5, 9) = 4 + 9 = 13
6 + max(9, 3) = 6 + 9 = 15
3
7 4
10 13 15
7 + max(10, 13) = 7 + 13 = 20
4 + max(13, 15) = 4 + 15 = 19
3
20 19
3 + max(20, 19) = 3 + 20 = 23
Áp dụng cách làm trên vào ma trận này:
3 0 0 0
7 4 0 0
2 4 6 0
8 5 9 3
2 + max(8, 5) = 2 + 8 = 10
==>GRID(2, 0) := GRID(2, 0) + max(GRID(3,0), GRID(3,1))
4 + max(5, 9) = 4 + 9 = 13
==>GRID(2, 1) := GRID(2, 1) + max(GRID(3,1), GRID(3,2))
6 + max(9, 3) = 6 + 9 = 15
==> GRID(2, 2) := GRID(2, 2) + max(GRID(3,2), GRID(3,3))
Công thức tổng quát:
GRID(x, y) := GRID(x, y) + max(GRID(x+1,y), GRID(x+1,y+1))
Áp dụng vào bài toán lớn hơn:
def calc_maximum_path_v1():
max_lenght = len(GIRD[0])
for x in range(max_lenght - 2, -1, -1):
for y in range(0, max_lenght):
if GIRD[x][y] != 0:
GIRD[x][y] = GIRD[x][y] + max(GIRD[x + 1][y], GIRD[x + 1][y + 1])
return GIRD[0][0]
Thời gian chạy bài toán
The maximum path sum: 1074
elapsed time: 8.821487426757812e-05s
Source-code: PE-018